


Next: Smoothed Aggregation
Up: Multigrid Background
Previous: Multigrid Background
Contents
AMG preconditioners
In order to describe the AMG preconditioners available in MLD2P4, we consider a
linear system
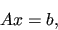 |
(2) |
where
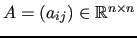 is a nonsingular sparse matrix;
for ease of presentation we assume
is a nonsingular sparse matrix;
for ease of presentation we assume 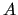 has a symmetric sparsity
pattern.
has a symmetric sparsity
pattern.
Let us consider as finest index space the set of row (column) indices of 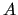 , i.e.,
, i.e.,
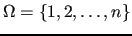 .
Any algebraic multilevel preconditioners implemented in MLD2P4 generates
a hierarchy of index spaces and a corresponding hierarchy of matrices,
.
Any algebraic multilevel preconditioners implemented in MLD2P4 generates
a hierarchy of index spaces and a corresponding hierarchy of matrices,
by using the information contained in 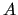 , without assuming any
knowledge of the geometry of the problem from which
, without assuming any
knowledge of the geometry of the problem from which 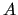 originates.
A vector space
originates.
A vector space
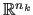 is associated with
is associated with 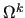 ,
where
,
where  is the size of
is the size of 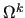 .
For all
.
For all 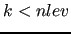 , a restriction operator and a prolongation one are built,
which connect two levels
, a restriction operator and a prolongation one are built,
which connect two levels 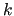 and
and 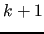 :
:
the matrix 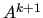 is computed by using the previous operators according
to the Galerkin approach, i.e.,
is computed by using the previous operators according
to the Galerkin approach, i.e.,
In the current implementation of MLD2P4 we have 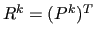 A smoother with iteration matrix
A smoother with iteration matrix 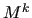 is set up at each level
is set up at each level 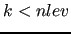 , and a solver
is set up at the coarsest level, so that they are ready for application
(for example, setting up a solver based on the
, and a solver
is set up at the coarsest level, so that they are ready for application
(for example, setting up a solver based on the 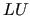 factorization means computing
and storing the
factorization means computing
and storing the 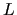 and
and 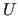 factors). The construction of the hierarchy of AMG components
described so far corresponds to the so-called build phase of the preconditioner.
factors). The construction of the hierarchy of AMG components
described so far corresponds to the so-called build phase of the preconditioner.
Figure 1:
Application phase of a V-cycle preconditioner.
|
|
The components produced in the build phase may be combined in several ways
to obtain different multilevel preconditioners;
this is done in the application phase, i.e., in the computation of a vector
of type 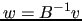 , where
, where 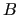 denotes the preconditioner, usually within an iteration
of a Krylov solver [20]. An example of such a combination, known as
V-cycle, is given in Figure 1. In this case, a single iteration
of the same smoother is used before and after the the recursive call to the V-cycle (i.e.,
in the pre-smoothing and post-smoothing phases); however, different choices can be
performed. Other cycles can be defined; in MLD2P4, we implemented the standard V-cycle
and W-cycle [3], and a version of the K-cycle described
in [19].
denotes the preconditioner, usually within an iteration
of a Krylov solver [20]. An example of such a combination, known as
V-cycle, is given in Figure 1. In this case, a single iteration
of the same smoother is used before and after the the recursive call to the V-cycle (i.e.,
in the pre-smoothing and post-smoothing phases); however, different choices can be
performed. Other cycles can be defined; in MLD2P4, we implemented the standard V-cycle
and W-cycle [3], and a version of the K-cycle described
in [19].



Next: Smoothed Aggregation
Up: Multigrid Background
Previous: Multigrid Background
Contents
![]() , i.e.,
, i.e.,
![]() .
Any algebraic multilevel preconditioners implemented in MLD2P4 generates
a hierarchy of index spaces and a corresponding hierarchy of matrices,
.
Any algebraic multilevel preconditioners implemented in MLD2P4 generates
a hierarchy of index spaces and a corresponding hierarchy of matrices,
![]() , where
, where ![]() denotes the preconditioner, usually within an iteration
of a Krylov solver [20]. An example of such a combination, known as
V-cycle, is given in Figure 1. In this case, a single iteration
of the same smoother is used before and after the the recursive call to the V-cycle (i.e.,
in the pre-smoothing and post-smoothing phases); however, different choices can be
performed. Other cycles can be defined; in MLD2P4, we implemented the standard V-cycle
and W-cycle [3], and a version of the K-cycle described
in [19].
denotes the preconditioner, usually within an iteration
of a Krylov solver [20]. An example of such a combination, known as
V-cycle, is given in Figure 1. In this case, a single iteration
of the same smoother is used before and after the the recursive call to the V-cycle (i.e.,
in the pre-smoothing and post-smoothing phases); however, different choices can be
performed. Other cycles can be defined; in MLD2P4, we implemented the standard V-cycle
and W-cycle [3], and a version of the K-cycle described
in [19].