


Next: Getting Started
Up: Multigrid Background
Previous: Multigrid Background
Contents
AMG preconditioners
In order to describe the AMG preconditioners available in MLD2P4, we consider a
linear system
 |
(2) |
where
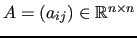 is a nonsingular sparse matrix;
for ease of presentation we assume
is a nonsingular sparse matrix;
for ease of presentation we assume 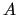 is real, but the
results are valid for the complex case as well.
Let us assume as finest index space the set of row (column) indices of
is real, but the
results are valid for the complex case as well.
Let us assume as finest index space the set of row (column) indices of 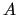 , i.e.,
, i.e.,
 .
Any algebraic multilevel preconditioners implemented in MLD2P4 generates
a hierarchy of index spaces and a corresponding hierarchy of matrices,
.
Any algebraic multilevel preconditioners implemented in MLD2P4 generates
a hierarchy of index spaces and a corresponding hierarchy of matrices,
by using the information contained in 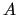 , without assuming any
knowledge of the geometry of the problem from which
, without assuming any
knowledge of the geometry of the problem from which 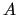 originates.
A vector space
originates.
A vector space
 is associated with
is associated with  ,
where
,
where  is the size of
is the size of  .
For all
.
For all 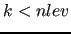 , a restriction operator and a prolongation one are built,
which connect two levels
, a restriction operator and a prolongation one are built,
which connect two levels 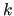 and
and  :
:



Next: Getting Started
Up: Multigrid Background
Previous: Multigrid Background
Contents