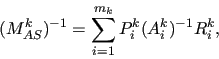


Next: Getting Started
Up: Multigrid Background
Previous: Smoothed Aggregation
Contents
Smoothers and coarsest-level solvers
The smoothers implemented in MLD2P4 include the Jacobi and block-Jacobi methods,
a hybrid version of the forward and backward Gauss-Seidel methods, and the
additive Schwarz (AS) ones (see, e.g., [20,21]).
The hybrid Gauss-Seidel
version is considered because the original Gauss-Seidel method is inherently sequential.
At each iteration of the hybrid version, each parallel process uses the most recent values
of its own local variables and the values of the non-local variables computed at the
previous iteration, obtained by exchanging data with other processes before
the beginning of the current iteration.
In the AS methods, the index space 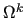 is divided into
is divided into 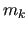 subsets
subsets 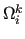 of size
of size 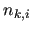 , possibly
overlapping. For each
, possibly
overlapping. For each 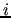 we consider the restriction
operator
we consider the restriction
operator
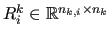 that maps a vector
that maps a vector 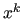 to the vector
to the vector 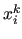 made of the components of
made of the components of 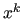 with indices in
with indices in 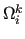 , and the prolongation operator
, and the prolongation operator
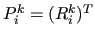 . These operators are then used to build
. These operators are then used to build
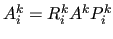 , which is the restriction of
, which is the restriction of 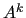 to the index
space
to the index
space 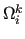 .
The classical AS preconditioner
.
The classical AS preconditioner 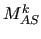 is defined as
is defined as
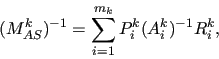
where 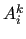 is supposed to be nonsingular. We observe that an approximate
inverse of
is supposed to be nonsingular. We observe that an approximate
inverse of 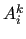 is usually considered instead of
is usually considered instead of 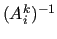 .
The setup of
.
The setup of 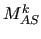 during the multilevel build phase
involves
during the multilevel build phase
involves
- the definition of the index subspaces
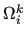 and of the corresponding
operators
and of the corresponding
operators 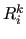 (and
(and 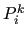 );
);
- the computation of the submatrices
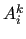 ;
;
- the computation of their inverses (usually approximated
through some form of incomplete factorization).
The computation of
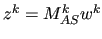 , with
, with
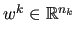 , during the
multilevel application phase, requires
, during the
multilevel application phase, requires
- the restriction of
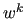 to the subspaces
to the subspaces
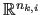 ,
i.e.
,
i.e.
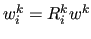 ;
;
- the computation of the vectors
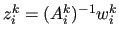 ;
;
- the prolongation and the sum of the previous vectors,
i.e.
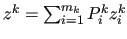 .
.
Variants of the classical AS method, which use modifications of the
restriction and prolongation operators, are also implemented in MLD2P4.
Among them, the Restricted AS (RAS) preconditioner usually
outperforms the classical AS preconditioner in terms of convergence
rate and of computation and communication time on parallel distributed-memory
computers, and is therefore the most widely used among the AS
preconditioners [6].
Direct solvers based on sparse LU factorizations, implemented in the
third-party libraries reported in Section 3.2, can be applied
as coarsest-level solvers by MLD2P4. Native inexact solvers based on
incomplete LU factorizations, as well as Jacobi, hybrid (forward) Gauss-Seidel,
and block Jacobi preconditioners are also available. Direct solvers usually
lead to more effective preconditioners in terms of algorithmic scalability;
however, this does not guarantee parallel efficiency.



Next: Getting Started
Up: Multigrid Background
Previous: Smoothed Aggregation
Contents