The Multilevel preconditioners implemented in MLD2P4 are obtained by combining AS preconditioners with coarse-space corrections; therefore we first provide a sketch of the AS preconditioners.
Given the linear system ,
where
![]() is a
nonsingular sparse matrix with a symmetric nonzero pattern,
let
is a
nonsingular sparse matrix with a symmetric nonzero pattern,
let ![]() be the adjacency graph of
be the adjacency graph of ![]() , where
, where
![]() and
and
![]() are the vertex set and the edge set of
are the vertex set and the edge set of ![]() ,
respectively. Two vertices are called adjacent if there is an edge connecting
them. For any integer
,
respectively. Two vertices are called adjacent if there is an edge connecting
them. For any integer ![]() , a
, a ![]() -overlap
partition of
-overlap
partition of ![]() can be defined recursively as follows.
Given a 0-overlap (or non-overlapping) partition of
can be defined recursively as follows.
Given a 0-overlap (or non-overlapping) partition of ![]() ,
i.e. a set of
,
i.e. a set of ![]() disjoint nonempty sets
disjoint nonempty sets
![]() such that
such that
![]() , a
, a ![]() -overlap
partition of
-overlap
partition of ![]() is obtained by considering the sets
is obtained by considering the sets
![]() obtained by including the vertices that
are adjacent to any vertex in
obtained by including the vertices that
are adjacent to any vertex in
![]() .
.
Let ![]() be the size of
be the size of ![]() and
and
![]() the restriction operator that maps
a vector
the restriction operator that maps
a vector ![]() onto the vector
onto the vector
![]() containing the components of
containing the components of ![]() corresponding to the vertices in
corresponding to the vertices in
![]() . The transpose of
. The transpose of ![]() is a
prolongation operator from
is a
prolongation operator from
![]() to
to ![]() .
The matrix
.
The matrix
![]() can be considered
as a restriction of
can be considered
as a restriction of ![]() corresponding to the set
corresponding to the set ![]() .
.
The classical one-level AS preconditioner is defined by
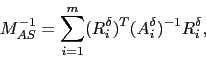
A variant of the classical AS preconditioner that outperforms it
in terms of convergence rate and of computation and communication
time on parallel distributed-memory computers is the so-called Restricted AS
(RAS) preconditioner [5,10]. It
is obtained by zeroing the components of ![]() corresponding to the
overlapping vertices when applying the prolongation. Therefore,
RAS differs from classical AS by the prolongation operators,
which are substituted by
corresponding to the
overlapping vertices when applying the prolongation. Therefore,
RAS differs from classical AS by the prolongation operators,
which are substituted by
![]() ,
where
,
where ![]() is obtained by zeroing the rows of
is obtained by zeroing the rows of ![]() corresponding to the vertices in
corresponding to the vertices in
![]() :
:
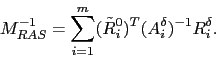
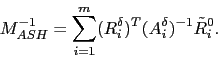
As already observed, the convergence rate of the one-level Schwarz
preconditioned iterative solvers deteriorates as the number ![]() of partitions
of
of partitions
of ![]() increases [7,15]. To reduce the dependency
of the number of iterations on the degree of parallelism we may
introduce a global coupling among the overlapping partitions by defining
a coarse-space approximation
increases [7,15]. To reduce the dependency
of the number of iterations on the degree of parallelism we may
introduce a global coupling among the overlapping partitions by defining
a coarse-space approximation ![]() of the matrix
of the matrix ![]() .
In a pure algebraic setting,
.
In a pure algebraic setting, ![]() is usually built with
a Galerkin approach. Given a set
is usually built with
a Galerkin approach. Given a set ![]() of coarse vertices,
with size
of coarse vertices,
with size ![]() , and a suitable restriction operator
, and a suitable restriction operator
![]() ,
, ![]() is defined as
is defined as
The combination of ![]() and
and ![]() may be
performed in either an additive or a multiplicative framework.
In the former case, the two-level additive Schwarz preconditioner
is obtained:
may be
performed in either an additive or a multiplicative framework.
In the former case, the two-level additive Schwarz preconditioner
is obtained:
In the multiplicative case, the combination can be
performed by first applying the smoother ![]() and then
the coarse-level correction operator
and then
the coarse-level correction operator ![]() :
:
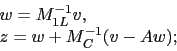
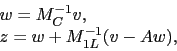
As previously noted, on parallel computers the number of submatrices usually matches
the number of available processors. When the size of the system to be preconditioned
is very large, the use of many processors, i.e. of many small submatrices, often
leads to a large coarse-level system, whose solution may be computationally expensive.
On the other hand, the use of few processors often leads to local sumatrices that
are too expensive to be processed on single processors, because of memory and/or
computing requirements. Therefore, it seems natural to use a recursive approach,
in which the coarse-level correction is re-applied starting from the current
coarse-level system. The corresponding preconditioners, called multi-level
preconditioners, can significantly reduce the computational cost of preconditioning
with respect to the two-level case (see [15, Chapter 3]).
Additive and hybrid multilevel preconditioners
are obtained as direct extensions of the two-level counterparts.
For a detailed descrition of them, the reader is
referred to [15, Chapter 3].
The algorithm for the application of a multi-level hybrid
post-smoothed preconditioner ![]() to a vector
to a vector ![]() , i.e. for the
computation of
, i.e. for the
computation of ![]() , is reported, for
example, in Figure
, is reported, for
example, in Figure ![]() . Here the number of levels
is denoted by
. Here the number of levels
is denoted by ![]() and the levels are numbered in increasing order starting
from the finest one, i.e. the finest level is level 1; the coarse matrix
and the corresponding basic preconditioner at each level
and the levels are numbered in increasing order starting
from the finest one, i.e. the finest level is level 1; the coarse matrix
and the corresponding basic preconditioner at each level ![]() are denoted by
are denoted by ![]() and
and
![]() , respectively, with
, respectively, with ![]() .
.