



Next: Examples
Up: userhtml
Previous: Smoothed Aggregation
Contents
Getting Started
We describe the basics for building and applying MLD2P4 one-level and multi-level
Schwarz preconditioners with the Krylov solvers included in PSBLAS [11].
The following steps are required:
- Declare the preconditioner data structure. It is a derived data type,
mld_xprec_type, where x may be s, d, c
or z, according to the basic data type of the sparse matrix
(s = real single precision; d = real double precision;
c = complex single precision; z = complex double precision).
This data structure is accessed by the user only through the MLD2P4 routines,
following an object-oriented approach.
- Allocate and initialize the preconditioner data structure, according to
a preconditioner type chosen by the user. This is performed by the routine
mld_precinit, which also sets defaults for each preconditioner
type selected by the user. The defaults associated to each preconditioner
type are given in Table ![[*]](file:/usr/share/latex2html/icons/crossref.png) , where the strings used by
, where the strings used by
mld_precinit to identify the preconditioner types are also given.
Note that these strings are valid also if uppercase letters are substituted by
corresponding lowercase ones.
- Modify the selected preconditioner type, by properly setting
preconditioner parameters. This is performed by the routine
mld_precset.
This routine must be called only if the user wants to modify the default values
of the parameters associated to the selected preconditioner type, to obtain a variant
of the preconditioner. Examples of use of mld_precset are given in
Section ![[*]](file:/usr/share/latex2html/icons/crossref.png) ; a complete list of all the
preconditioner parameters and their allowed and default values is provided in
Section
; a complete list of all the
preconditioner parameters and their allowed and default values is provided in
Section ![[*]](file:/usr/share/latex2html/icons/crossref.png) , Tables
, Tables ![[*]](file:/usr/share/latex2html/icons/crossref.png) -
-![[*]](file:/usr/share/latex2html/icons/crossref.png) .
.
- Build the preconditioner for a given matrix. This is performed by
the routine
mld_precbld.
- Apply the preconditioner at each iteration of a Krylov solver.
This is performed by the routine
mld_precaply. When using the PSBLAS Krylov solvers,
this step is completely transparent to the user, since mld_precaply is called
by the PSBLAS routine implementing the Krylov solver (psb_krylov).
- Free the preconditioner data structure. This is performed by
the routine
mld_precfree. This step is complementary to step 1 and should
be performed when the preconditioner is no more used.
A detailed description of the above routines is given in Section ![[*]](file:/usr/share/latex2html/icons/crossref.png) .
Examples showing the basic use of MLD2P4 are reported in Section
.
Examples showing the basic use of MLD2P4 are reported in Section ![[*]](file:/usr/share/latex2html/icons/crossref.png) .
.
Note that the Fortran 95 module mld_prec_mod, containing the definition of the
preconditioner data type and the interfaces to the routines of MLD2P4,
must be used in any program calling such routines.
The modules psb_base_mod, for the sparse matrix and communication descriptor
data types, and psb_krylov_mod, for interfacing with the
Krylov solvers, must be also used (see Section ![[*]](file:/usr/share/latex2html/icons/crossref.png) ).
).
Remark 1. The coarsest-level solver used by the default two-level
preconditioner has been chosen by taking into account that, on parallel
machines, it often leads to the smallest execution time when applied to
linear systems coming from finite-difference discretizations of basic
elliptic PDE problems, considered as standard tests for multi-level Schwarz
preconditioners [3,4]. However, this solver does
not necessarily correspond to the smallest number of iterations of the
preconditioned Krylov method, which is usually obtained by applying
a direct solver to the coarsest-level system, e.g. based on the LU
factorization (see Section ![[*]](file:/usr/share/latex2html/icons/crossref.png) for the coarsest-level solvers available in MLD2P4).
for the coarsest-level solvers available in MLD2P4).
Remark 2. The include path for MLD2P4 must override
those for PSBLAS, e.g. the latter must come first in the sequence
passed to the compiler, as the MLD2P4 version of the Krylov solver
interfaces must override that of PSBLAS. This will change in the future
when the support for the class statement becomes widespread in Fortran
compilers.
Table:
Preconditioner types, corresponding strings and default choices.
| TYPE |
STRING |
DEFAULT PRECONDITIONER |
| No preconditioner |
'NOPREC' |
Considered only to use the PSBLAS
Krylov solvers with no preconditioner. |
| Diagonal |
'DIAG' |
-- |
| Block Jacobi |
'BJAC' |
Block Jacobi with ILU(0) on the local blocks. |
| Additive Schwarz |
'AS' |
Restricted Additive Schwarz (RAS),
with overlap 1 and ILU(0) on the local blocks. |
| Multilevel |
'ML' |
Multi-level hybrid preconditioner (additive on the
same level and multiplicative through the levels),
with post-smoothing only.
Number of levels: 2.
Post-smoother: RAS with overlap 1 and ILU(0)
on the local blocks.
Aggregation: smoothed aggregation with
threshold 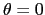 .
Coarsest matrix: distributed among the processors.
Coarsest-level solver:
4 sweeps of the block-Jacobi solver,
with LU factorization of the blocks
(UMFPACK for the double precision versions and
SuperLU for the single precision ones) .
Coarsest matrix: distributed among the processors.
Coarsest-level solver:
4 sweeps of the block-Jacobi solver,
with LU factorization of the blocks
(UMFPACK for the double precision versions and
SuperLU for the single precision ones) |
|
Subsections




Next: Examples
Up: userhtml
Previous: Smoothed Aggregation
Contents
Salvatore Filippone
2008-07-22