Next: Getting Started Up: Multigrid Background Previous: Smoothed Aggregation Contents
The smoothers implemented in MLD2P4 include the Jacobi and block-Jacobi methods, a hybrid version of the forward and backward Gauss-Seidel methods, and the additive Schwarz (AS) ones (see, e.g., [20,21]).
The hybrid Gauss-Seidel version is considered because the original Gauss-Seidel method is inherently sequential. At each iteration of the hybrid version, each parallel process uses the most recent values of its own local variables and the values of the non-local variables computed at the previous iteration, obtained by exchanging data with other processes before the beginning of the current iteration.
In the AS methods, the index space ![]() is divided into
is divided into ![]() subsets
subsets ![]() of size
of size ![]() , possibly
overlapping. For each
, possibly
overlapping. For each ![]() we consider the restriction
operator
we consider the restriction
operator
![]() that maps a vector
that maps a vector ![]() to the vector
to the vector ![]() made of the components of
made of the components of ![]() with indices in
with indices in ![]() , and the prolongation operator
, and the prolongation operator
![]() . These operators are then used to build
. These operators are then used to build
![]() , which is the restriction of
, which is the restriction of ![]() to the index
space
to the index
space ![]() .
The classical AS preconditioner
.
The classical AS preconditioner ![]() is defined as
is defined as
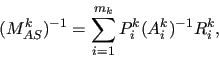
Direct solvers based on sparse LU factorizations, implemented in the third-party libraries reported in Section 3.2, can be applied as coarsest-level solvers by MLD2P4. Native inexact solvers based on incomplete LU factorizations, as well as Jacobi, hybrid (forward) Gauss-Seidel, and block Jacobi preconditioners are also available. Direct solvers usually lead to more effective preconditioners in terms of algorithmic scalability; however, this does not guarantee parallel efficiency.