


Next: Subroutine build
Up: User Interface
Previous: Subroutine init
Contents
Subroutine set
call p%set(what,val,info [,ilev, ilmax, pos])
This routine sets the parameters defining the preconditioner p. More
precisely, the parameter identified by what is assigned the value
contained in val.
Arguments
what |
character(len=*). |
| |
The parameter to be set. It can be specified by
a predefined constant, or through its name; the string
is case-insensitive. See also
Tables 2-8. |
val |
integer or character(len=*) or
real(psb_spk_) or real(psb_dpk_),
intent(in). |
| |
The value of the parameter to be set. The list of allowed
values and the corresponding data types is given in
Tables 2-8.
When the value is of type character(len=*),
it is also treated as case insensitive. |
info |
integer, intent(out). |
| |
Error code. If no error, 0 is returned. See Section 8
for details. |
ilev |
integer, optional, intent(in). |
| |
For the multi-level preconditioner, the level at which the
preconditioner parameter has to be set.
The levels are numbered in increasing
order starting from the finest one, i.e., level 1 is the finest level.
If ilev is not present, the parameter identified by what
is set at all the appropriate levels (see
Tables 2-8). |
ilmax |
integer, optional, intent(in). |
| |
For the multi-level preconditioner, when both
ilev and ilmax are present, the settings
are applied at all levels ilev:ilmax. When
ilev is present but ilmax is not, then
the default is ilmax=ilev.
The levels are numbered in increasing
order starting from the finest one, i.e., level 1 is the finest level. |
pos |
charater(len=*), optional, intent(in). |
| |
Whether the other arguments apply only to the pre-smoother ('PRE')
or to the post-smoother ('POST'). If pos is not present,
the other arguments are applied to both smoothers.
If the preconditioner is one-level or the parameter identified by what
does not concern the smoothers, pos is ignored. |
For compatibility with the previous versions of MLD2P4, this routine can be also invoked
as follows:
call mld_precset(p,what,val,info)
However, in this case the optional arguments ilev, ilmax, and pos
cannot be used.
A variety of preconditioners can be obtained
by a suitable setting of the preconditioner parameters. These parameters
can be logically divided into four groups, i.e., parameters defining
- the type of multi-level cycle and how many cycles must be applied;
- the aggregation algorithm;
- the coarse-space correction at the coarsest level (for multi-level
preconditioners only);
- the smoother of the multi-level preconditioners, or the one-level
preconditioner.
A list of the parameters that can be set, along with their allowed and
default values, is given in Tables 2-8.
For a description of the meaning of the parameters, please
refer also to Section 4.
Remark 2. A smoother is usually obtained by combining two objects:
a smoother (SMOOTHER_TYPE) and a local solver (SUB_SOLVE),
as specified in Tables 7-8.
For example, the block-Jacobi smoother using
ILU(0) on the blocks is obtained by combining the block-Jacobi smoother
object with the ILU(0) solver object. Similarly,
the hybrid Gauss-Seidel smoother (see Note in Table 7)
is obtained by combining the block-Jacobi smoother object with a single sweep
of the Gauss-Seidel solver object, while the point-Jacobi smoother is the
result of combining the block-Jacobi smoother object with a single sweep
of the pointwise-Jacobi solver object. However, for simplicity, shortcuts are
provided to set point-Jacobi, hybrid (forward) Gauss-Seidel, and
hybrid backward Gauss-Seidel, i.e., the previous smoothers can be defined
by setting only SMOOTHER_TYPE to appropriate values (see
Tables 7), i.e., without setting
SUB_SOLVE too.
The smoother and solver objects are arranged in a
hierarchical manner. When specifying a smoother object, its parameters,
including the local solver, are set to their default values, and when a solver
object is specified, its defaults are also set, overriding in both
cases any previous settings even if explicitly specified. Therefore if
the user sets a smoother, and wishes to use a solver
different from the default one, the call to set the solver must come
after the call to set the smoother.
Similar considerations apply to the point-Jacobi, Gauss-Seidel and block-Jacobi
coarsest-level solvers, and shortcuts are available
in this case too (see Table 5).
Remark 3. In general, a coarsest-level solver cannot be used with
both the replicated and distributed coarsest-matrix layout;
therefore, setting the solver after the layout may change the layout.
Similarly, setting the layout after the solver may change the solver.
More precisely, UMFPACK and SuperLU require the coarsest-level
matrix to be replicated, while SuperLU_Dist requires it to be distributed.
In these cases, setting the coarsest-level solver implies that
the layout is redefined according to the solver, ovverriding any
previous settings. MUMPS, point-Jacobi,
hybrid Gauss-Seidel and block-Jacobi can be applied to
replicated and distributed matrices, thus their choice
does not modify any previously specified layout.
It is worth noting that, when the matrix is replicated,
the point-Jacobi, hybrid Gauss-Seidel and block-Jacobi solvers
reduce to the corresponding local solver objects (see Remark 2).
For the point-Jacobi and Gauss-Seidel solvers, these objects
correspond to a single point-Jacobi sweep and a single
Gauss-Seidel sweep, respectively, which are very poor solvers.
On the other hand, the distributed layout can be used with any solver
but UMFPACK and SuperLU; therefore, if any of these two solvers has already
been selected, the coarsest-level solver is changed to block-Jacobi,
with the previously chosen solver applied to the local blocks.
Likewise, the replicated layout can be used with any solver but SuperLu_Dist;
therefore, if SuperLu_Dist has been previously set, the coarsest-level
solver is changed to the default sequential solver.
Table 2:
Parameters defining the multi-level cycle and the number of cycles to
be applied.
what |
DATA TYPE |
val |
DEFAULT |
COMMENTS |
ML_CYCLE |
character(len=*) |
'VCYCLE'
'WCYCLE'
'KCYCLE'
'MULT'
'ADD' |
'VCYCLE' |
Multi-level cycle: V-cycle, W-cycle, K-cycle, hybrid Multiplicative Schwarz,
and Additive Schwarz.
Note that hybrid Multiplicative Schwarz is equivalent to V-cycle and
is included for compatibility with previous versions of MLD2P4. |
OUTER_SWEEPS |
integer |
Any integer
number 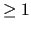 |
1 |
Number of multi-level cycles. |
|
Table 3:
Parameters defining the aggregation algorithm.
what |
DATA TYPE |
val |
DEFAULT |
COMMENTS |
MIN_COARSE_SIZE |
integer |
Any number
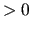 |
![$\lfloor 40 \sqrt[3]{n} \rfloor$](img19.png) , where , where 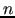 is the dimension
of the matrix at the finest level is the dimension
of the matrix at the finest level |
Coarse size threshold. The aggregation stops
if the global number of variables of the
computed coarsest matrix
is lower than or equal to this threshold
(see Note). |
MIN_CR_RATIO |
real |
Any number
 |
1.5 |
Minimum coarsening ratio. The aggregation stops
if the ratio between the matrix dimensions
at two consecutive levels is lower than or equal to this
threshold (see Note). |
MAX_LEVS |
integer |
Any integer
number  |
20 |
Maximum number of levels. The aggregation stops
if the number of levels reaches this value (see Note). |
PAR_AGGR |
character(len=*) |
'DEC', 'SYMDEC' |
'DEC' |
Parallel aggregation algorithm.
Currently, only the
decoupled aggregation (DEC) is available; the
SYMDEC option applies decoupled
aggregation to the sparsity pattern
of  . . |
AGGR_TYPE |
character(len=*) |
'VMB' |
'VMB' |
Type of aggregation algorithm: currently, the scalar aggregation
algorithm by Vanek, Mandel and Brezina is implemented
[29]. |
AGGR_PROL |
character(len=*) |
'SMOOTHED', 'UNSMOOTHED' |
'SMOOTHED' |
Prolongator used by the aggregation algorithm: smoothed or unsmoothed
(i.e., tentative prolongator). |
| Note. The aggregation algorithm stops when
at least one of the following criteria is met:
the coarse size threshold, the |
| maximum coarsening ratio, or the maximum number
of levels is reached. Therefore, the actual number of levels may be |
| smaller than the specified maximum number
of levels. |
|
Table 4:
Parameters defining the aggregation algorithm (continued).
|
|
Table 5:
Parameters defining the coarse-space correction at the coarsest
level.
what |
DATA TYPE |
val |
DEFAULT |
COMMENTS |
COARSE_MAT |
character(len=*) |
'DIST'
'REPL' |
'REPL' |
Coarsest matrix layout: distributed among the processes or
replicated on each of them. |
COARSE_SOLVE |
character(len=*) |
'MUMPS'
'UMF'
'SLU'
'SLUDIST'
'JACOBI'
'GS'
'BJAC' |
See Note. |
Solver used at the coarsest level: sequential
LU from MUMPS, UMFPACK, or SuperLU
(plus triangular solve);
distributed LU from MUMPS or SuperLU_Dist
(plus triangular solve);
point-Jacobi, hybrid Gauss-Seidel or block-Jacobi.
Note that UMF and SLU require the coarsest
matrix to be replicated, SLUDIST, JACOBI,
GS and BJAC require it to be
distributed, MUMPS can be used with either
a replicated or a distributed matrix. When any of the previous
solvers is specified, the matrix layout is set to a default
value
which allows the use
value UMFPACK and SuperLU_Dist
are available only in double precision. |
COARSE_SUBSOLVE |
character(len=*) |
'ILU'
'ILUT'
'MILU'
'MUMPS'
'SLU'
'UMF' |
See Note. |
Solver for the diagonal blocks of the coarse matrix,
in case the block Jacobi solver
is chosen as coarsest-level solver: ILU(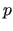 ), ILU( ), ILU( ),
MILU( ),
MILU(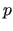 ), LU from MUMPS, SuperLU or UMFPACK
(plus triangular solve).
Note that UMFPACK and SuperLU_Dist
are available only in double precision. ), LU from MUMPS, SuperLU or UMFPACK
(plus triangular solve).
Note that UMFPACK and SuperLU_Dist
are available only in double precision. |
| Note. Defaults for COARSE_SOLVE and
COARSE_SUBSOLVE are chosen in the following order: |
| single precision version - MUMPS if installed,
then SLU if installed,
ILU otherwise; |
| double precision version - UMF if installed,
then MUMPS if installed, then SLU if
installed, ILU otherwise. |
|
Table 6:
Parameters defining the coarse-space correction at the coarsest
level (continued).
|
|
Table 7:
Parameters defining the smoother or the details of the one-level preconditioner.
what |
DATA TYPE |
val |
DEFAULT |
COMMENTS |
SMOOTHER_TYPE |
character(len=*)
|
'JACOBI'
'GS'
'BGS'
'BJAC'
'AS'
|
'FBGS'
|
Type of smoother used in the multi-level preconditioner:
point-Jacobi, hybrid (forward) Gauss-Seidel,
hybrid backward Gauss-Seidel, block-Jacobi, and
Additive Schwarz.
It is ignored by one-level preconditioners. |
SUB_SOLVE |
character(len=*)
|
'JACOBI'
'GS'
'BGS'
'ILU'
'ILUT'
'MILU'
'MUMPS'
'SLU'
'UMF'
|
GS and BGS for pre- and post-smoothers
of multi-level preconditioners, respectively
ILU for block-Jacobi and Additive Schwarz
one-level preconditioners
|
The local solver to be used with the smoother or one-level
preconditioner (see Remark 2, page 24): point-Jacobi,
hybrid (forward) Gauss-Seidel, hybrid backward
Gauss-Seidel, ILU(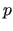 ), ILU( ), ILU( ), MILU( ), MILU(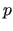 ),
LU from MUMPS, SuperLU or UMFPACK
(plus triangular solve). See Note for details on hybrid
Gauss-Seidel. ),
LU from MUMPS, SuperLU or UMFPACK
(plus triangular solve). See Note for details on hybrid
Gauss-Seidel. |
SMOOTHER_SWEEPS |
integer
|
Any integer
number 
|
1
|
Number of sweeps of the smoother or one-level preconditioner.
In the multi-level case, no pre-smother or
post-smoother is used if this parameter is set to 0
together with pos='PRE' or pos='POST,
respectively. |
SUB_OVR |
integer
|
Any integer
number 
|
1
|
Number of overlap layers, for Additive Schwarz only. |
|
Table 8:
Parameters defining the smoother or the details of the one-level preconditioner
(continued).
what |
DATA TYPE |
val |
DEFAULT |
COMMENTS |
SUB_RESTR |
character(len=*)
|
'HALO'
'NONE'
|
'HALO'
|
Type of restriction operator, for Additive Schwarz only:
HALO for taking into account the overlap, NONE
for neglecting it.
Note that HALO must be chosen for
the classical Addditive Schwarz smoother and its RAS variant. |
SUB_PROL |
character(len=*)
|
'SUM'
'NONE'
|
'NONE'
|
Type of prolongation operator, for Additive Schwarz only:
SUM for adding the contributions from the overlap, NONE
for neglecting them.
Note that SUM must be chosen for the classical Additive
Schwarz smoother, and NONE for its RAS variant. |
SUB_FILLIN |
integer
|
Any integer
number 
|
0
|
Fill-in level 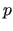 of the incomplete LU factorizations. of the incomplete LU factorizations. |
SUB_ILUTHRS |
real(kind_parameter)
|
Any real number 
|
0
|
Drop tolerance  in the ILU( in the ILU( ) factorization. ) factorization. |
| |
|
|
|
|
|



Next: Subroutine build
Up: User Interface
Previous: Subroutine init
Contents