Smoothed Aggregation
In order to define the prolongator 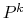 , used to compute
the coarse-level matrix
, used to compute
the coarse-level matrix 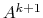 , MLD2P4 uses the smoothed aggregation
algorithm described in [2,26].
The basic idea of this algorithm is to build a coarse set of indices
, MLD2P4 uses the smoothed aggregation
algorithm described in [2,26].
The basic idea of this algorithm is to build a coarse set of indices
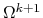 by suitably grouping the indices of
by suitably grouping the indices of 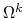 into disjoint
subsets (aggregates), and to define the coarse-to-fine space transfer operator
into disjoint
subsets (aggregates), and to define the coarse-to-fine space transfer operator
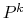 by applying a suitable smoother to a simple piecewise constant
prolongation operator, with the aim of improving the quality of the coarse-space correction.
by applying a suitable smoother to a simple piecewise constant
prolongation operator, with the aim of improving the quality of the coarse-space correction.
Three main steps can be identified in the smoothed aggregation procedure:
- aggregation of the indices of
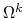 to obtain
to obtain 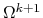 ;
;
- construction of the prolongator
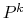 ;
;
- application of
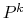 and
and 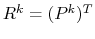 to build
to build 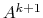 .
.
In order to perform the coarsening step, the smoothed aggregation algorithm
described in [26] is used. In this algorithm,
each index
 corresponds to an aggregate
corresponds to an aggregate 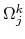 of
of 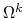 ,
consisting of a suitably chosen index
,
consisting of a suitably chosen index
 and indices that are (usually) contained in a
strongly-coupled neighborood of
and indices that are (usually) contained in a
strongly-coupled neighborood of 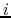 , i.e.,
, i.e.,
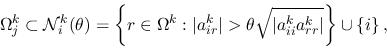 |
(3) |
for a given threshold
![$\theta \in [0,1]$](img32.png) (see [26] for the details).
Since this algorithm has a sequential nature, a decoupled
version of it is applied, where each processor independently executes
the algorithm on the set of indices assigned to it in the initial data
distribution. This version is embarrassingly parallel, since it does not require any data
communication. On the other hand, it may produce some nonuniform aggregates
and is strongly dependent on the number of processors and on the initial partitioning
of the matrix
(see [26] for the details).
Since this algorithm has a sequential nature, a decoupled
version of it is applied, where each processor independently executes
the algorithm on the set of indices assigned to it in the initial data
distribution. This version is embarrassingly parallel, since it does not require any data
communication. On the other hand, it may produce some nonuniform aggregates
and is strongly dependent on the number of processors and on the initial partitioning
of the matrix 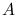 . Nevertheless, this parallel algorithm has been chosen for
MLD2P4, since it has been shown to produce good results in practice
[5,7,25].
. Nevertheless, this parallel algorithm has been chosen for
MLD2P4, since it has been shown to produce good results in practice
[5,7,25].
The prolongator 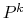 is built starting from a tentative prolongator
is built starting from a tentative prolongator
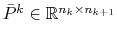 , defined as
, defined as
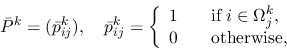 |
(4) |
where 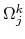 is the aggregate of
is the aggregate of 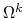 corresponding to the index
corresponding to the index
 .
.
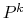 is obtained by applying to
is obtained by applying to  a smoother
a smoother
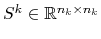 :
:
in order to remove nonsmooth components from the range of the prolongator,
and hence to improve the convergence properties of the multilevel
method [2,24].
A simple choice for 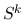 is the damped Jacobi smoother:
is the damped Jacobi smoother:
where 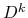 is the diagonal matrix with the same diagonal entries as
is the diagonal matrix with the same diagonal entries as 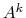 ,
,
 is the filtered matrix defined as
is the filtered matrix defined as
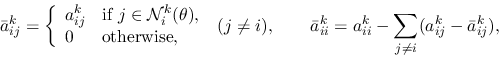 |
(5) |
and  is an approximation of
is an approximation of 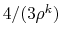 , where
, where
 is the spectral radius of
is the spectral radius of
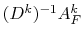 [2].
In MLD2P4 this approximation is obtained by using
[2].
In MLD2P4 this approximation is obtained by using
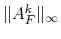 as an estimate
of
as an estimate
of  . Note that for systems coming from uniformly elliptic
problems, filtering the matrix
. Note that for systems coming from uniformly elliptic
problems, filtering the matrix 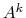 has little or no effect, and
has little or no effect, and
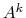 can be used instead of
can be used instead of 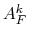 . The latter choice is the default in MLD2P4.
. The latter choice is the default in MLD2P4.
![]() , used to compute
the coarse-level matrix
, used to compute
the coarse-level matrix ![]() , MLD2P4 uses the smoothed aggregation
algorithm described in [2,26].
The basic idea of this algorithm is to build a coarse set of indices
, MLD2P4 uses the smoothed aggregation
algorithm described in [2,26].
The basic idea of this algorithm is to build a coarse set of indices
![]() by suitably grouping the indices of
by suitably grouping the indices of ![]() into disjoint
subsets (aggregates), and to define the coarse-to-fine space transfer operator
into disjoint
subsets (aggregates), and to define the coarse-to-fine space transfer operator
![]() by applying a suitable smoother to a simple piecewise constant
prolongation operator, with the aim of improving the quality of the coarse-space correction.
by applying a suitable smoother to a simple piecewise constant
prolongation operator, with the aim of improving the quality of the coarse-space correction.
![]() corresponds to an aggregate
corresponds to an aggregate ![]() of
of ![]() ,
consisting of a suitably chosen index
,
consisting of a suitably chosen index
![]() and indices that are (usually) contained in a
strongly-coupled neighborood of
and indices that are (usually) contained in a
strongly-coupled neighborood of ![]() , i.e.,
, i.e.,
![]() is built starting from a tentative prolongator
is built starting from a tentative prolongator
![]() , defined as
, defined as