Smoothers and coarsest-level solvers

The smoothers implemented in MLD2P4 include the Jacobi and block-Jacobi methods, a hybrid version of the forward and backward Gauss-Seidel methods, and the additive Schwarz (AS) ones (see, e.g., [21,22]).

The hybrid Gauss-Seidel version is considered because the original Gauss-Seidel method is inherently sequential. At each iteration of the hybrid version, each parallel process uses the most recent values of its own local variables and the values of the non-local variables computed at the previous iteration, obtained by exchanging data with other processes before the beginning of the current iteration.

In the AS methods, the index space $\Omega^k$ is divided into $m_k$ subsets $\Omega^k_i$ of size $n_{k,i}$, possibly overlapping. For each $i$ we consider the restriction operator $R_i^k \in \mathbb{R}^{n_{k,i} \times n_k}$ that maps a vector $x^k$ to the vector $x_i^k$ made of the components of $x^k$ with indices in $\Omega^k_i$, and the prolongation operator $P^k_i = (R_i^k)^T$. These operators are then used to build $A_i^k=R_i^kA^kP_i^k$, which is the restriction of $A^k$ to the index space $\Omega^k_i$. The classical AS preconditioner $M^k_{AS}$ is defined as

$$( M^k_{AS} )^{-1} = \sum_{i=1}^{m_k} P_i^k (A_i^k)^{-1} R_i^{k},$$

where $A_i^k$ is supposed to be nonsingular. We observe that an approximate inverse of $A_i^k$ is usually considered instead of $(A_i^k)^{-1}$. The setup of $M^k_{AS}$ during the multilevel build phase involves

• the definition of the index subspaces $\Omega_i^k$ and of the corresponding operators $R_i^k$ (and $P_i^k$);
• the computation of the submatrices $A_i^k$;
• the computation of their inverses (usually approximated through some form of incomplete factorization).

The computation of $z^k=M^k_{AS}w^k$, with $w^k \in \mathbb{R}^{n_k}$, during the multilevel application phase, requires

• the restriction of $w^k$ to the subspaces $\mathbb{R}^{n_{k,i}}$, i.e. $w_i^k = R_i^{k} w^k$;
• the computation of the vectors $z_i^k=(A_i^k)^{-1} w_i^k$;
• the prolongation and the sum of the previous vectors, i.e. $z^k = \sum_{i=1}^{m_k} P_i^k z_i^k$.

Variants of the classical AS method, which use modifications of the restriction and prolongation operators, are also implemented in MLD2P4. Among them, the Restricted AS (RAS) preconditioner usually outperforms the classical AS preconditioner in terms of convergence rate and of computation and communication time on parallel distributed-memory computers, and is therefore the most widely used among the AS preconditioners [6].

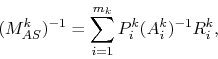
Direct solvers based on sparse LU factorizations, implemented in the third-party libraries reported in Section 3.2, can be applied as coarsest-level solvers by MLD2P4. Native inexact solvers based on incomplete LU factorizations, as well as Jacobi, hybrid (forward) Gauss-Seidel, and block Jacobi preconditioners are also available. Direct solvers usually lead to more effective preconditioners in terms of algorithmic scalability; however, this does not guarantee parallel efficiency.