Dense Vector Data Structure

The vdatapsb_vect_type data structure contains all information about local portion of the sparse matrix and its storage mode. Most of these fields are set by the tools routines when inserting a new sparse matrix; the user needs only choose, if he/she so whishes, a specific matrix storage mode.

aspk

Contains values of the local distributed sparse matrix.
Specified as: an allocatable array of rank one of type corresponding to matrix entries type.

ia1

Holds integer information on distributed sparse matrix. Actual information will depend on data format used.
Specified as: an allocatable integer array of rank one.

ia2

Holds integer information on distributed sparse matrix. Actual information will depend on data format used.
Specified as: an allocatable integer array of rank one.

infoa

On entry can hold auxiliary information on distributed sparse matrix. Actual information will depend on data format used.
Specified as: an integer array of length psb_ifasize_.

fida

Defines the format of the distributed sparse matrix.
Specified as: a string of length 5

descra

Describe the characteristic of the distributed sparse matrix.
Specified as: array of character of length 9.

pl

Specifies the local row permutation of distributed sparse matrix. If pl(1) is equal to 0, then there isn't row permutation.
Specified as: an allocatable integer array of dimension equal to number of local row (matrix_data[psb_n_row_])

pr

Specifies the local column permutation of distributed sparse matrix. If PR(1) is equal to 0, then there isn't columnm permutation.
Specified as: an allocatable integer array of dimension equal to number of local row (matrix_data[psb_n_col_])

m

Number of rows; if row indices are stored explicitly, as in Coordinate Storage, should be greater than or equal to the maximum row index actually present in the sparse matrix. Specified as: integer variable.

k

Number of columns; if column indices are stored explicitly, as in Coordinate Storage or Compressed Sparse Rows, should be greater than or equal to the maximum column index actually present in the sparse matrix. Specified as: integer variable.

The Fortran 95 interface for distributed sparse matrices containing double precision real entries is defined as shown in figure 5. The definitions for single precision and complex data are identical except for the real declaration and for the kind type parameter.

Figure 5: The PSBLAS defined data type that contains a sparse matrix.

The following two cases are among the most commonly used:

fida=``CSR''

Compressed storage by rows. In this case the following should hold:

1. ia2(i) contains the index of the first element of row i; the last element of the sparse matrix is thus stored at index 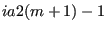$ia2(m+1)-1$. It should contain m+1 entries in nondecreasing order (strictly increasing, if there are no empty rows).
2. ia1(j) contains the column index and aspk(j) contains the corresponding coefficient value, for all $ia2(1) \le j \le ia2(m+1)-1$.

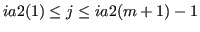fida=``COO''

Coordinate storage. In this case the following should hold:

1. infoa(1) contains the number of nonzero elements in the matrix;
2. For all $1 \le j \le infoa(1)$, the coefficient, row index and column index are stored into apsk(j), ia1(j) and ia2(j) respectively.

A sparse matrix has an associated state, which can take the following values:

Build:

State entered after the first allocation, and before the first assembly; in this state it is possible to add nonzero entries.

Assembled:

State entered after the assembly; computations using the sparse matrix, such as matrix-vector products, are only possible in this state;

Update:

State entered after a reinitalization; this is used to handle applications in which the same sparsity pattern is used multiple times with different coefficients. In this state it is only possible to enter coefficients for already existing nonzero entries.