You cannot select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
1.6 KiB
1.6 KiB
Homotopy Continuation in Julia
This is a project for the "Laboratorio Computazionale" exam at the University of Pisa
Implemented
- Total-degree Homotopy with "Roots of unity" start system
- Euler-Newton predictor-corrector method with adaptive step size
- Homotopy Continuation for all roots of the target system
TODO
- [~] Parallelization
Homogenization
Example systems
Here's some tests on 2x2 systems, with the plotted real approximate solutions
\begin{align*}
x^3 + 5x^2 - y - 10 &= 0 \\
2x^2 - y - 10 &= 0 \\
\end{align*}
| Single-threaded | Multi-threaded (nproc=6) |
|---|---|
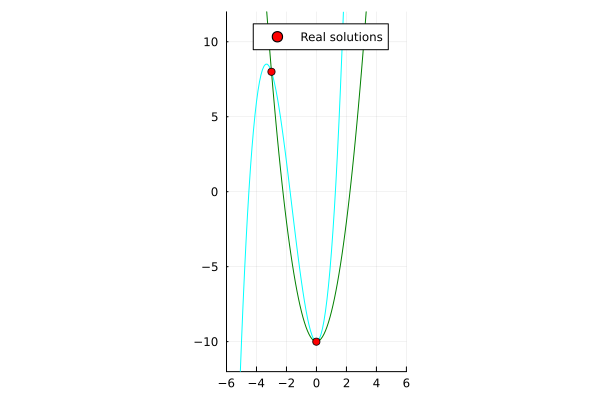 |
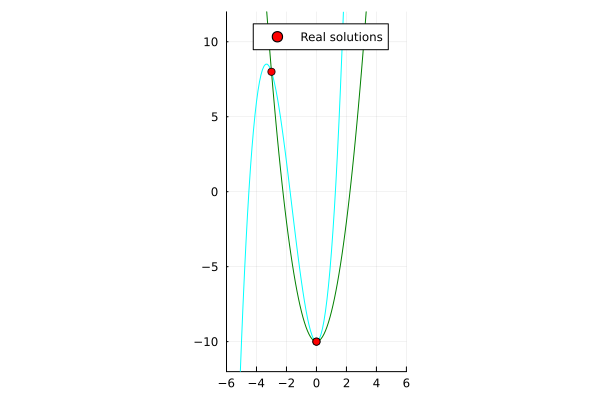 |
\begin{align*}
x^2 + 2y &= 0 \\
y - 3x^3 &= 0 \\
\end{align*}
| Single-threaded | Multi-threaded (nproc=6) |
|---|---|
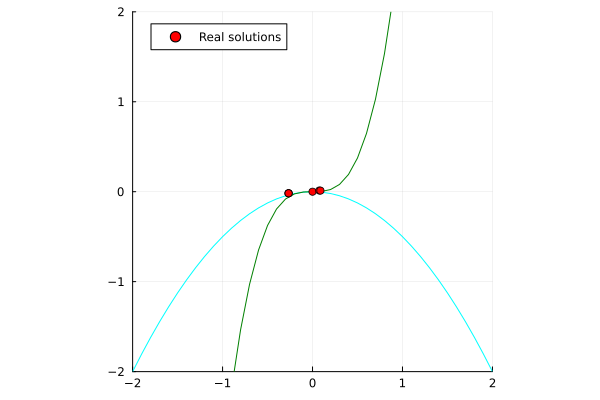 |
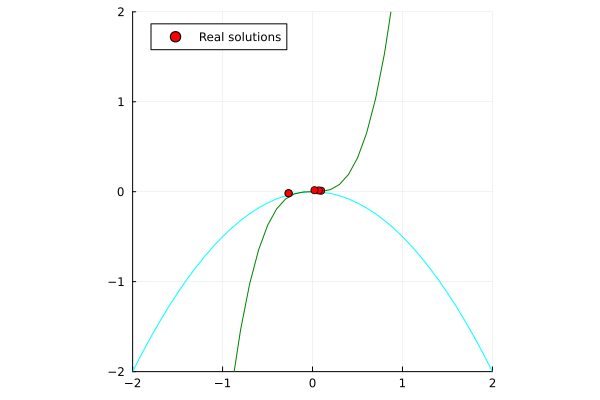 |
\begin{align*}
x^2 + y^2 - 4 &= 0 \\
xy - 1 &= 0 \\
\end{align*}
| Single-threaded | Multi-threaded (nproc=6) |
|---|---|
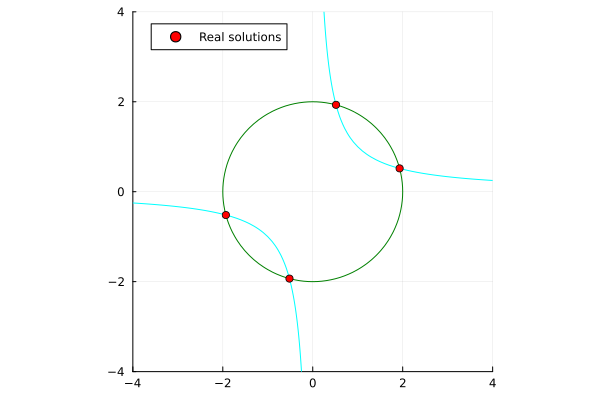 |
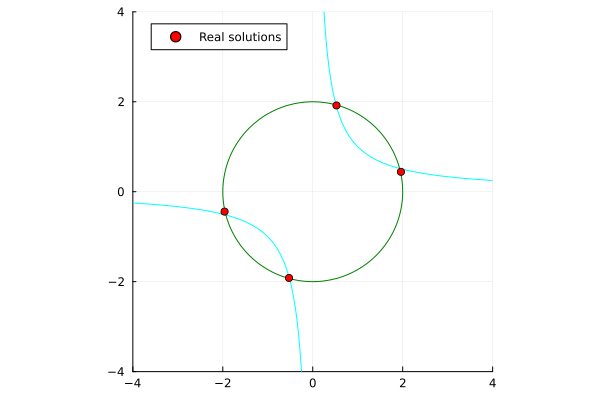 |
\begin{align*}
x^2 + y^2 - 2 &= 0 \\
xy - 1 &= 0 \\
\end{align*}
| Single-threaded | Multi-threaded (nproc=6) |
|---|---|
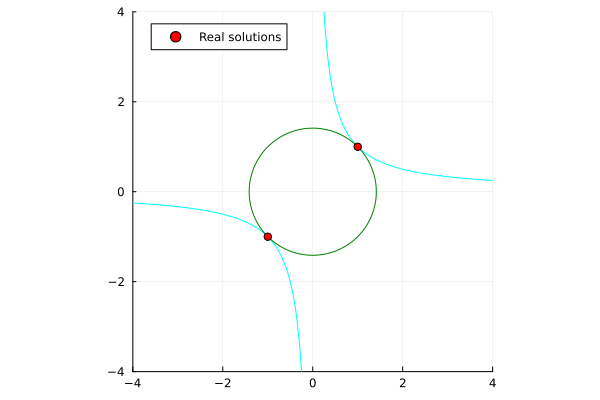 |
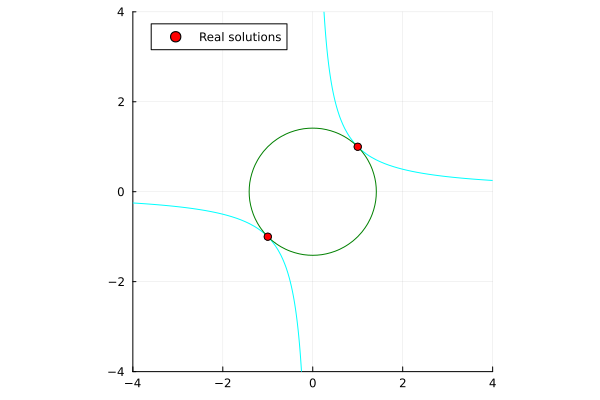 |