![]()
The PSBLAS library is designed to handle the implementation of iterative solvers for sparse linear systems on distributed memory parallel computers. The system coefficient matrix A must be square; it may be real or complex, nonsymmetric, and its sparsity pattern needs not to be symmetric. The serial computation parts are based on the serial sparse BLAS, so that any extension made to the data structures of the serial kernels is available to the parallel version. The overall design and parallelization strategy have been influenced by the structure of the ScaLAPACK parallel library. The layered structure of the PSBLAS library is shown in figure 1; lower layers of the library indicate an encapsulation relationship with upper layers. The ongoing discussion focuses on the Fortran 2003 layer immediately below the application layer. The serial parts of the computation on each process are executed through calls to the serial sparse BLAS subroutines. In a similar way, the inter-process message exchanges are encapsulated in an applicaiton layer that has been strongly inspired by the Basic Linear Algebra Communication Subroutines (BLACS) library [6]. Usually there is no need to deal directly with MPI; however, in some cases, MPI routines are used directly to improve efficiency. For further details on our communication layer see Sec. 7.
The type of linear system matrices that we address typically arise in the numerical solution of PDEs; in such a context, it is necessary to pay special attention to the structure of the problem from which the application originates. The nonzero pattern of a matrix arising from the discretization of a PDE is influenced by various factors, such as the shape of the domain, the discretization strategy, and the equation/unknown ordering. The matrix itself can be interpreted as the adjacency matrix of the graph associated with the discretization mesh.
The distribution of the coefficient matrix for the linear system is based on the “owner computes” rule: the variable associated to each mesh point is assigned to a process that will own the corresponding row in the coefficient matrix and will carry out all related computations. This allocation strategy is equivalent to a partition of the discretization mesh into sub-domains. Our library supports any distribution that keeps together the coefficients of each matrix row; there are no other constraints on the variable assignment. This choice is consistent with simple data distributions such as CYCLIC(N) and BLOCK, as well as completely arbitrary assignments of equation indices to processes. In particular it is consistent with the usage of graph partitioning tools commonly available in the literature, e.g. METIS [13]. Dense vectors conform to sparse matrices, that is, the entries of a vector follow the same distribution of the matrix rows.
We assume that the sparse matrix is built in parallel, where each process generates its own portion. We never require that the entire matrix be available on a single node. However, it is possible to hold the entire matrix in one process and distribute it explicitly1 , even though the resulting memory bottleneck would make this option unattractive in most cases.
Our computational model implies that the data allocation on the parallel distributed memory machine is guided by the structure of the physical model, and specifically by the discretization mesh of the PDE.
Each point of the discretization mesh will have (at least) one associated equation/variable, and therefore one index. We say that point i depends on point j if the equation for a variable associated with i contains a term in j, or equivalently if aij≠0. After the partition of the discretization mesh into sub-domains assigned to the parallel processes, we classify the points of a given sub-domain as following.
Internal.
An internal point of a given domain depends only on points of the same domain. If all points of a domain are assigned to one process, then a computational step (e.g., a matrix-vector product) of the equations associated with the internal points requires no data items from other domains and no communications.
Boundary.
A point of a given domain is a boundary point if it depends on points belonging to other domains.
Halo.
A halo point for a given domain is a point belonging to another domain such that there is a boundary point which depends on it. Whenever performing a computational step, such as a matrix-vector product, the values associated with halo points are requested from other domains. A boundary point of a given domain is usually a halo point for some other domain2 ; therefore the cardinality of the boundary points set denotes the amount of data sent to other domains.
Overlap.
An overlap point is a boundary point assigned to multiple domains. Any operation that involves an overlap point has to be replicated for each assignment.
Overlap points do not usually exist in the basic data distributions; however they are a feature of Domain Decomposition Schwarz preconditioners which are the subject of related research work [3, 2].
We denote the sets of internal, boundary and halo points for a given subdomain
by 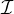 ,
, 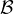 and
and 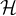 . Each subdomain is assigned to one process; each process usually owns
one subdomain, although the user may choose to assign more than one subdomain to
a process. If each process i owns one subdomain, the number of rows in
the local sparse matrix is |
. Each subdomain is assigned to one process; each process usually owns
one subdomain, although the user may choose to assign more than one subdomain to
a process. If each process i owns one subdomain, the number of rows in
the local sparse matrix is |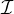 i| + |
i| + |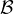 i|, and the number of local columns (i.e.
those for which there exists at least one non-zero entry in the local rows) is
|
i|, and the number of local columns (i.e.
those for which there exists at least one non-zero entry in the local rows) is
|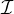 i| + |
i| + |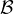 i| + |
i| + |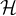 i|.
i|.
This classification of mesh points guides the naming scheme that we adopted in the library internals and in the data structures. We explicitly note that “Halo” points are also often called “ghost” points in the literature.
The PSBLAS library consists of various classes of subroutines:
Computational routines
comprising:
Sparse matrix by dense matrix product;
Sparse triangular systems solution for block diagonal matrices;
Vector and matrix norms;
Dense matrix sums;
Dot products.
Communication routines
handling halo and overlap communications;
Data management and auxiliary routines
including:
Parallel environment management
Communication descriptors allocation;
Dense and sparse matrix allocation;
Dense and sparse matrix build and update;
Sparse matrix and data distribution preprocessing.
Preconditioner routines
Iterative methods
a subset of Krylov subspace iterative methods
The following naming scheme has been adopted for all the symbols internally defined in the PSBLAS software package:
all symbols (i.e. subroutine names, data types...) are prefixed by psb_
all data type names are suffixed by _type
all constants are suffixed by _
all top-level subroutine names follow the rule psb_xxname where xx can be either:
ge: the routine is related to dense data,
sp: the routine is related to sparse data,
cd: the routine is related to communication descriptor (see 3).
For example the psb_geins, psb_spins and psb_cdins perform the same action (see 6) on dense matrices, sparse matrices and communication descriptors respectively. Interface overloading allows the usage of the same subroutine names for both real and complex data.
In the description of the subroutines, arguments or argument entries are classified as:
global
For input arguments, the value must be the same on all processes participating in the subroutine call; for output arguments the value is guaranteed to be the same.
local
Each process has its own value(s) independently.
To finish our general description, we define a version string with the constant
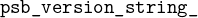
whose current value is 3.8.0
The main underlying principle of the PSBLAS library is that the library objects are created and exist with reference to a discretized space to which there corresponds an index space and a matrix sparsity pattern. As an example, consider a cell-centered finite-volume discretization of the Navier-Stokes equations on a simulation domain; the index space 1…n is isomorphic to the set of cell centers, whereas the pattern of the associated linear system matrix is isomorphic to the adjacency graph imposed on the discretization mesh by the discretization stencil.
Thus the first order of business is to establish an index space, and this is done with a call to psb_cdall in which we specify the size of the index space n and the allocation of the elements of the index space to the various processes making up the MPI (virtual) parallel machine.
The index space is partitioned among processes, and this creates a mapping from the “global” numbering 1…n to a numbering “local” to each process; each process i will own a certain subset 1…nrowi, each element of which corresponds to a certain element of 1…n. The user does not set explicitly this mapping; when the application needs to indicate to which element of the index space a certain item is related, such as the row and column index of a matrix coefficient, it does so in the “global” numbering, and the library will translate into the appropriate “local” numbering.
For a given index space 1…n there are many possible associated topologies, i.e. many different discretization stencils; thus the description of the index space is not completed until the user has defined a sparsity pattern, either explicitly through psb_cdins or implicitly through psb_spins. The descriptor is finalized with a call to psb_cdasb and a sparse matrix with a call to psb_spasb. After psb_cdasb each process i will have defined a set of “halo” (or “ghost”) indices nrowi + 1…ncol i, denoting elements of the index space that are not assigned to process i; however the variables associated with them are needed to complete computations associated with the sparse matrix A, and thus they have to be fetched from (neighbouring) processes. The descriptor of the index space is built exactly for the purpose of properly sequencing the communication steps required to achieve this objective.
A simple application structure will walk through the index space allocation, matrix/vector creation and linear system solution as follows:
Initialize parallel environment with psb_init
Initialize index space with psb_cdall
Allocate sparse matrix and dense vectors with psb_spall and psb_geall
Loop over all local rows, generate matrix and vector entries, and insert them with psb_spins and psb_geins
Assemble the various entities:
psb_cdasb
psb_spasb
psb_geasb
Choose the preconditioner to be used with prec%init and build it with prec%build3 .
Call the iterative driver psb_krylov with the method of choice, e.g. bicgstab.
This is the structure of the sample programs in the directory test/pargen/.
For a simulation in which the same discretization mesh is used over multiple time steps, the following structure may be more appropriate:
Initialize parallel environment with psb_init
Initialize index space with psb_cdall
Loop over the topology of the discretization mesh and build the descriptor with psb_cdins
Assemble the descriptor with psb_cdasb
Allocate the sparse matrices and dense vectors with psb_spall and psb_geall
Loop over the time steps:
If after first time step, reinitialize the sparse matrix with psb_sprn; also zero out the dense vectors;
Loop over the mesh, generate the coefficients and insert/update them with psb_spins and psb_geins
Assemble with psb_spasb and psb_geasb
Choose and build preconditioner with prec%init and prec%build
Call the iterative method of choice, e.g. psb_bicgstab
The insertion routines will be called as many times as needed; they only need to be called on the data that is actually allocated to the current process, i.e. each process generates its own data.
In principle there is no specific order in the calls to psb_spins, nor is there a requirement to build a matrix row in its entirety before calling the routine; this allows the application programmer to walk through the discretization mesh element by element, generating the main part of a given matrix row but also contributions to the rows corresponding to neighbouring elements.
From a functional point of view it is even possible to execute one call for each nonzero coefficient; however this would have a substantial computational overhead. It is therefore advisable to pack a certain amount of data into each call to the insertion routine, say touching on a few tens of rows; the best performng value would depend on both the architecture of the computer being used and on the problem structure. At the opposite extreme, it would be possible to generate the entire part of a coefficient matrix residing on a process and pass it in a single call to psb_spins; this, however, would entail a doubling of memory occupation, and thus would be almost always far from optimal.
PSBLAS supports user-defined global to local index mappings, subject to the constraints outlined in sec. 2.3:
The set of indices owned locally must be mapped to the set 1…nrowi;
The set of halo points must be mapped to the set nrowi + 1…ncol i;
but otherwise the mapping is arbitrary. The user application is responsible to ensure consistency of this mapping; some errors may be caught by the library, but this is not guaranteed. The application structure to support this usage is as follows:
Initialize index space with psb_cdall(ictx,desc,info,vl=vl,lidx=lidx) passing the vectors vl(:) containing the set of global indices owned by the current process and lidx(:) containing the corresponding local indices;
Add the halo points ja(:) and their associated local indices lidx(:) with a(some) call(s) to psb_cdins(nz,ja,desc,info,lidx=lidx);
Assemble the descriptor with psb_cdasb;
Build the sparse matrices and vectors, optionally making use in psb_spins and psb_geins of the local argument specifying that the indices in ia, ja and irw, respectively, are already local indices.
The PSBLAS librarary is based on the Single Program Multiple Data (SPMD) programming model: each process participating in the computation performs the same actions on a chunk of data. Parallelism is thus data-driven.
Because of this structure, many subroutines coordinate their action across the various processes, thus providing an implicit synchronization point, and therefore must be called simultaneously by all processes participating in the computation. This is certainly true for the data allocation and assembly routines, for all the computational routines and for some of the tools routines.
However there are many cases where no synchronization, and indeed no communication among processes, is implied; for instance, all the routines in sec. 3 are only acting on the local data structures, and thus may be called independently. The most important case is that of the coefficient insertion routines: since the number of coefficients in the sparse and dense matrices varies among the processors, and since the user is free to choose an arbitrary order in builiding the matrix entries, these routines cannot imply a synchronization.
Throughout this user’s guide each subroutine will be clearly indicated as:
Synchronous:
must be called simultaneously by all the processes in the relevant communication context;
Asynchronous:
may be called in a totally independent manner.