psb_ovrl — Overlap Update

5.2 psb_ovrl — Overlap Update

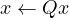
These subroutines applies an overlap operator to the input vector:

x ← Qx

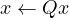
where:

x: is the global dense submatrix x
Q: is the overlap operator; it is the composition of two operators P_a and P^T.


x	Subroutine

Short Precision Real	psb_ovrl
Long Precision Real	psb_ovrl
Short Precision Complex	psb_ovrl
Long Precision Complex	psb_ovrl

Table 18: Data types

call psb_ovrl(x, desc_a, info)
call psb_ovrl(x, desc_a, info, update=update_type, work=work)

Type:

Synchronous.

On Entry

x

global dense matrix x.
Scope: local
Type: required
Intent: inout.
Specified as: a rank one or two array or an object of type psb_T_vect_type containing numbers of type specified in Table 18.

desc_a

contains data structures for communications.
Scope: local
Type: required
Intent: in.
Specified as: a structured data of type psb_desc_type.

update

Update operator.

update = psb_none_: Do nothing;
update = psb_add_: Sum overlap entries, i.e. apply P^T;
update = psb_avg_: Average overlap entries, i.e. apply P_aP^T;

Scope: global
Intent: in.
Default: update_type = psb_avg_
Scope: global
Specified as: a integer variable.

work

the work array.
Scope: local
Type: optional
Intent: inout.
Specified as: a one dimensional array of the same type of x.

On Return

x

global dense result matrix x.
Scope: local
Type: required
Intent: inout.
Specified as: an array of rank one or two containing numbers of type specified in Table 18.

info

Error code.
Scope: local
Type: required
Intent: out.
An integer value; 0 means no error has been detected.

Notes

If there is no overlap in the data distribution associated with the descriptor, no operations are performed;
The operator P^T performs the reduction sum of overlap elements; it is a “prolongation” operator P^T that replicates overlap elements, accounting for the physical replication of data;
The operator P_a performs a scaling on the overlap elements by the amount of replication; thus, when combined with the reduction operator, it implements the average of replicated elements over all of their instances.

Figure 4: Sample discretization mesh.

Example of use Consider the discretization mesh depicted in fig. 4, partitioned among two processes as shown by the dashed lines, with an overlap of 1 extra layer with respect to the partition of fig. 3; the data distribution is such that each process will own 40 entries in the index space, with an overlap of 16 entries placed at local indices 25 through 40; the halo will run from local index 41 through local index 48.. If process 0 assigns an initial value of 1 to its entries in the x vector, and process 1 assigns a value of 2, then after a call to psb_ovrl with psb_avg_ and a call to psb_halo_ the contents of the local vectors will be the following (showing a transition among the two subdomains)

Process 0			Process 1
I	GLOB(I)	X(I)	I	GLOB(I)	X(I)
1	1	1.0	1	33	1.5
2	2	1.0	2	34	1.5
3	3	1.0	3	35	1.5
4	4	1.0	4	36	1.5
5	5	1.0	5	37	1.5
6	6	1.0	6	38	1.5
7	7	1.0	7	39	1.5
8	8	1.0	8	40	1.5
9	9	1.0	9	41	2.0
10	10	1.0	10	42	2.0
11	11	1.0	11	43	2.0
12	12	1.0	12	44	2.0
13	13	1.0	13	45	2.0
14	14	1.0	14	46	2.0
15	15	1.0	15	47	2.0
16	16	1.0	16	48	2.0
17	17	1.0	17	49	2.0
18	18	1.0	18	50	2.0
19	19	1.0	19	51	2.0
20	20	1.0	20	52	2.0
21	21	1.0	21	53	2.0
22	22	1.0	22	54	2.0
23	23	1.0	23	55	2.0
24	24	1.0	24	56	2.0
25	25	1.5	25	57	2.0
26	26	1.5	26	58	2.0
27	27	1.5	27	59	2.0
28	28	1.5	28	60	2.0
29	29	1.5	29	61	2.0
30	30	1.5	30	62	2.0
31	31	1.5	31	63	2.0
32	32	1.5	32	64	2.0
33	33	1.5	33	25	1.5
34	34	1.5	34	26	1.5
35	35	1.5	35	27	1.5
36	36	1.5	36	28	1.5
37	37	1.5	37	29	1.5
38	38	1.5	38	30	1.5
39	39	1.5	39	31	1.5
40	40	1.5	40	32	1.5
41	41	2.0	41	17	1.0
42	42	2.0	42	18	1.0
43	43	2.0	43	19	1.0
44	44	2.0	44	20	1.0
45	45	2.0	45	21	1.0
46	46	2.0	46	22	1.0
47	47	2.0	47	23	1.0
48	48	2.0	48	24	1.0

[next] [prev] [prev-tail] [front] [up]