On Return
Function value
The number of local rows, i.e. the number of rows owned by the current
process; as explained in 1, it is equal to |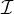 i| + |
i| + |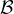 i|. The returned value is
specific to the calling process.
i|. The returned value is
specific to the calling process.
In this chapter we illustrate the data structures used for definition of routines interfaces. They include data structures for sparse matrices, communication descriptors and preconditioners.
All the data types and the basic subroutine interfaces related to descriptors and
sparse matrices are defined in the module psb_base_mod; this will have to be
included by every user subroutine that makes use of the library. The preconditioners
are defined in the module psb_prec_mod
Integer, real and complex data types are parametrized with a kind type defined in the library as follows:
psb_spk_
Kind parameter for short precision real and complex data; corresponds to
a REAL declaration and is normally 4 bytes;
psb_dpk_
Kind parameter for long precision real and complex data; corresponds to
a DOUBLE PRECISION declaration and is normally 8 bytes;
psb_mpk_
Kind parameter for 4-bytes integer data, as is always used by MPI;
psb_epk_
Kind parameter for 8-bytes integer data, as is always used by the sizeof
methods;
psb_ipk_
Kind parameter for “local” integer indices and data; with default build options this is a 4 bytes integer;
psb_lpk_
Kind parameter for “global” integer indices and data; with default build options this is an 8 bytes integer;
The integer kinds for local and global indices can be chosen at configure time to hold 4 or 8 bytes, with the global indices at least as large as the local ones. Together with the classes attributes we also discuss their methods. Most methods detailed here only act on the local variable, i.e. their action is purely local and asynchronous unless otherwise stated. The list of methods here is not completely exhaustive; many methods, especially those that alter the contents of the various objects, are usually not needed by the end-user, and therefore are described in the developer’s documentation.
All the general matrix informations and elements to be exchanged among processes are stored within a data structure of the type psb_desc_type. Every structure of this type is associated with a discretization pattern and enables data communications and other operations that are necessary for implementing the various algorithms of interest to us.
The data structure itself psb_desc_type can be treated as an opaque object
handled via the tools routines of Sec. 6 or the query routines detailed below;
nevertheless we include here a description for the curious reader.
First we describe the psb_indx_map type. This is a data structure that keeps
track of a certain number of basic issues such as:
The value of the communication context;
The number of indices in the index space, i.e. global number of rows and columns of a sparse matrix;
The local set of indices, including:
The number of local indices (and local rows);
The number of halo indices (and therefore local columns);
The global indices corresponding to the local ones.
There are many different schemes for storing these data; therefore there are a number of types extending the base one, and the descriptor structure holds a polymorphic object whose dynamic type can be any of the extended types. The methods associated with this data type answer the following queries:
For a given set of local indices, find the corresponding indices in the global numbering;
For a given set of global indices, find the corresponding indices in the local numbering, if any, or return an invalid
Add a global index to the set of halo indices;
Find the process owner of each member of a set of global indices.
All methods but the last are purely local; the last method potentially requires communication among processes, and thus is a synchronous method. The choice of a specific dynamic type for the index map is made at the time the descriptor is initially allocated, according to the mode of initialization (see also 6).
The descriptor contents are as follows:
indxmap
A polymorphic variable of a type that is any extension of the indx_map
type described above.
halo_index
A list of the halo and boundary elements for the current process to be exchanged with other processes; for each processes with which it is necessary to communicate:
Process identifier;
Number of points to be received;
Indices of points to be received;
Number of points to be sent;
Indices of points to be sent;
Specified as: a vector of integer type, see 3.3.
ext_index
A list of element indices to be exchanged to implement the mapping between a
base descriptor and a descriptor with overlap.
Specified as: a vector of integer type, see 3.3.
ovrlap_index
A list of the overlap elements for the current process, organized in groups like the previous vector:
Process identifier;
Number of points to be received;
Indices of points to be received;
Number of points to be sent;
Indices of points to be sent;
Specified as: a vector of integer type, see 3.3.
ovr_mst_idx
A list to retrieve the value of each overlap element from the respective master
process.
Specified as: a vector of integer type, see 3.3.
ovrlap_elem
For all overlap points belonging to th ecurrent process:
Overlap point index;
Number of processes sharing that overlap points;
Index of a “master” process:
Specified as: an allocatable integer array of rank two.
bnd_elem
A list of all boundary points, i.e. points that have a connection with other processes.
The Fortran 2003 declaration for psb_desc_type structures is as follows:
type psb_desc_type class(psb_indx_map), allocatable :: indxmap type(psb_i_vect_type) :: v_halo_index type(psb_i_vect_type) :: v_ext_index type(psb_i_vect_type) :: v_ovrlap_index type(psb_i_vect_type) :: v_ovr_mst_idx integer, allocatable :: ovrlap_elem(:,:) integer, allocatable :: bnd_elem(:) end type psb_desc_type
A communication descriptor associated with a sparse matrix has a state, which can take the following values:
Build:
State entered after the first allocation, and before the first assembly; in this state it is possible to add communication requirements among different processes.
Assembled:
State entered after the assembly; computations using the associated sparse matrix, such as matrix-vector products, are only possible in this state.
nr = desc%get_local_rows()
Type:
Asynchronous.
On Entry
desc
the communication descriptor.
Scope: local.
On Return
Function value
The number of local rows, i.e. the number of rows owned by the current
process; as explained in 1, it is equal to |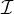 i| + |
i| + |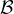 i|. The returned value is
specific to the calling process.
i|. The returned value is
specific to the calling process.
nc = desc%get_local_cols()
Type:
Asynchronous.
On Entry
desc
the communication descriptor.
Scope: local.
On Return
Function value
The number of local cols, i.e. the number of indices used by the current
process, including both local and halo indices; as explained in 1, it is equal
to |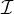 i| + |
i| + |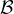 i| + |
i| + |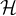 i|. The returned value is specific to the calling process.
i|. The returned value is specific to the calling process.
nr = desc%get_global_rows()
Type:
Asynchronous.
On Entry
desc
the communication descriptor.
Scope: local.
On Return
Function value
The number of global rows, i.e. the size of the global index space.
nr = desc%get_global_cols()
Type:
Asynchronous.
On Entry
desc
the communication descriptor.
Scope: local.
On Return
Function value
The number of global cols; usually this is equal to the number of global rows.
myidx = desc%get_global_indices([owned])
Type:
Asynchronous.
On Entry
desc
the communication descriptor.
Scope: local.
Type: required.
owned
Choose if you only want owned indices (owned=.true.) or also halo indices
(owned=.false.). Scope: local.
Type: optional; default: .true..
On Return
Function value
The global indices, returned as an allocatable integer array of kind
psb_lpk_ and rank 1.
ctxt = desc%get_context()
Type:
Asynchronous.
On Entry
desc
the communication descriptor.
Scope: local.
On Return
Function value
The communication context.
call desc%clone(descout,info)
Type:
Asynchronous.
On Entry
desc
the communication descriptor.
Scope: local.
On Return
descout
A copy of the input object.
info
Return code.
call desc%cnv(mold)
Type:
Asynchronous.
On Entry
desc
the communication descriptor.
Scope: local.
mold
the desired integer storage format.
Scope: local.
Specified as: a object of type derived from (integer)
psb_T_base_vect_type.
The mold arguments may be employed to interface with special devices, such as GPUs
and other accelerators.
ith = psb_cd_get_large_threshold()
Type:
Asynchronous.
On Return
Function value
The current value for the size threshold.
call psb_cd_set_large_threshold(ith)
Type:
Synchronous.
On Entry
ith
the new threshold for communication descriptors.
Scope: global.
Type: required.
Intent: in.
Specified as: an integer value greater than zero.
Note: the threshold value is only queried by the library at the time a call to psb_cdall
is executed, therefore changing the threshold has no effect on communication
descriptors that have already been initialized. Moreover the threshold must have the
same value on all processes.
list = desc%get_p_adjcncy()
Type:
Asynchronous.
On Return
Function value
The current list of adjacent processes, i.e. processes with which the current one has to exchange halo data.
call desc%set_p_adjcncy(list)
Type:
Asynchronous.
On Entry
list
the list of adjacent processes.
Scope: local.
Type: required.
Intent: in.
Specified as: a one-dimensional array of integers of kind psb_ipk_.
Note: this method can be called after a call to psb_cdall and before a call to
psb_cdasb. The user is specifying here some knowledge about which processes are
topological neighbours of the current process. The availability of this information
may speed up the execution of the assembly call psb_cdasb.
call desc%fnd_owner(idx,iprc,info)
Type:
Synchronous.
On Entry
idx
the list of global indices for which we need the owning processes.
Scope: local.
Type: required.
Intent: in.
Specified as: a one-dimensional array of integers of kind psb_lpk_.
On Return
iprc
the list of processes owning the indices in idx.
Scope: local.
Type: required.
Intent: in.
Specified as: an allocatable one-dimensional array of integers of kind
psb_ipk_.
Note: this method may or may not actually require communications, depending on the exact internal data storage; given that the choice of storage may be altered by runtime parameters, it is necessary for safety that this method is called by all processes.
psb_none_
Generic no-op;
psb_root_
Default root process for broadcast and scatter operations;
psb_nohalo_
Do not fetch halo elements;
psb_halo_
Fetch halo elements from neighbouring processes;
psb_sum_
Sum overlapped elements
psb_avg_
Average overlapped elements
psb_comm_halo_
Exchange data based on the halo_index list;
psb_comm_ext_
Exchange data based on the ext_index list;
psb_comm_ovr_
Exchange data based on the ovrlap_index list;
psb_comm_mov_
Exchange data based on the ovr_mst_idx list;
The psb_Tspmat_type class contains all information about the local portion of the
sparse matrix and its storage mode. Its design is based on the STATE design
pattern [12] as detailed in [10]; the type declaration is shown in figure 2 where T is a
placeholder for the data type and precision variants
S
Single precision real;
D
Double precision real;
C
Single precision complex;
Z
Double precision complex;
LS,LD,LC,LZ
Same numeric type as above, but with psb_lpk_ integer indices.
The actual data is contained in the polymorphic component a%a of type
psb_T_base_sparse_mat; its specific layout can be chosen dynamically among the
predefined types, or an entirely new storage layout can be implemented and passed to
the library at runtime via the psb_spasb routine.
type :: psb_Tspmat_type class(psb_T_base_sparse_mat), allocatable :: a end type psb_Tspmat_type
The following very common formats are precompiled in PSBLAS and thus are always available:
psb_T_coo_sparse_mat
Coordinate storage;
psb_T_csr_sparse_mat
Compressed storage by rows;
psb_T_csc_sparse_mat
Compressed storage by columns;
The inner sparse matrix has an associated state, which can take the following values:
Build:
State entered after the first allocation, and before the first assembly; in this state it is possible to add nonzero entries.
Assembled:
State entered after the assembly; computations using the sparse matrix, such as matrix-vector products, are only possible in this state;
Update:
State entered after a reinitalization; this is used to handle applications in which the same sparsity pattern is used multiple times with different coefficients. In this state it is only possible to enter coefficients for already existing nonzero entries.
The only storage variant supporting the build state is COO; all other variants are obtained by conversion to/from it.
nr = a%get_nrows()
Type:
Asynchronous.
On Entry
a
the sparse matrix
Scope: local
On Return
Function value
The number of rows of sparse matrix a.
nc = a%get_ncols()
Type:
Asynchronous.
On Entry
a
the sparse matrix
Scope: local
On Return
Function value
The number of columns of sparse matrix a.
nz = a%get_nnzeros()
Type:
Asynchronous.
On Entry
a
the sparse matrix
Scope: local
On Return
Function value
The number of nonzero elements stored in sparse matrix a.
Notes
The function value is specific to the storage format of matrix a; some
storage formats employ padding, thus the returned value for the same
matrix may be different for different storage choices.
maxnz = a%get_size()
Type:
Asynchronous.
On Entry
a
the sparse matrix
Scope: local
On Return
Function value
The maximum number of nonzero elements that can be stored in sparse
matrix a using its current memory allocation.
memory_size = a%sizeof()
Type:
Asynchronous.
On Entry
a
the sparse matrix
Scope: local
On Return
Function value
The memory occupation in bytes.
write(*,*) a%get_fmt()
Type:
Asynchronous.
On Entry
a
the sparse matrix
Scope: local
On Return
Function value
A short string describing the dynamic type of the matrix. Predefined values
include NULL, COO, CSR and CSC.
if (a%is_bld()) thenif (a%is_upd()) thenif (a%is_asb()) then
Type:
Asynchronous.
On Entry
a
the sparse matrix
Scope: local
On Return
Function value
A logical value indicating whether the matrix is in the Build, Update or
Assembled state, respectively.
if (a%is_triangle()) then if (a%is_upper()) then if (a%is_lower()) then if (a%is_unit()) then
Type:
Asynchronous.
On Entry
a
the sparse matrix
Scope: local
On Return
Function value
A logical value indicating whether the matrix is triangular; if
is_triangle() returns .true. check also if it is lower, upper and with a
unit (i.e. assumed) diagonal.
call a%cscnv(b,info [, type, mold, dupl]) call a%cscnv(info [, type, mold, dupl])
Type:
Asynchronous.
On Entry
a
the sparse matrix.
A variable of type psb_Tspmat_type.
Scope: local.
type
a string requesting a new format.
Type: optional.
mold
a variable of class(psb_T_base_sparse_mat) requesting a new format.
Type: optional.
dupl
an integer value specifing how to handle duplicates (see Named Constants below)
On Return
b,a
A copy of a with a new storage format.
A variable of type psb_Tspmat_type.
info
Return code.
The mold arguments may be employed to interface with special devices, such as GPUs
and other accelerators.
call a%csclip(b,info[,& & imin,imax,jmin,jmax,rscale,cscale])
Returns the submatrix A(imin:imax,jmin:jmax), optionally rescaling row/col
indices to the range 1:imax-imin+1,1:jmax-jmin+1.
Type:
Asynchronous.
On Entry
a
the sparse matrix.
A variable of type psb_Tspmat_type.
Scope: local.
imin,imax,jmin,jmax
Minimum and maximum row and column indices.
Type: optional.
rscale,cscale
Whether to rescale row/column indices. Type: optional.
On Return
b
A copy of a submatrix of a.
A variable of type psb_Tspmat_type.
info
Return code.
call a%clean_zeros(info)
Eliminates zero coefficients in the input matrix. Note that depending on the internal storage format, there may still be some amount of zero padding in the output.
Type:
Asynchronous.
On Entry
a
the sparse matrix.
A variable of type psb_Tspmat_type.
Scope: local.
On Return
a
The matrix a without zero coefficients.
A variable of type psb_Tspmat_type.
info
Return code.
call a%get_diag(d,info)
Returns a copy of the main diagonal.
Type:
Asynchronous.
On Entry
a
the sparse matrix.
A variable of type psb_Tspmat_type.
Scope: local.
On Return
d
A copy of the main diagonal.
A one-dimensional array of the appropriate type.
info
Return code.
call a%clip_diag(b,info)
Returns a copy of a without the main diagonal.
Type:
Asynchronous.
On Entry
a
the sparse matrix.
A variable of type psb_Tspmat_type.
Scope: local.
On Return
b
A copy of a without the main diagonal.
A variable of type psb_Tspmat_type.
info
Return code.
call a%tril(l,info[,& & diag,imin,imax,jmin,jmax,rscale,cscale,u])
Returns the lower triangular part of submatrix A(imin:imax,jmin:jmax),
optionally rescaling row/col indices to the range 1:imax-imin+1,1:jmax-jmin+1 and
returing the complementary upper triangle.
Type:
Asynchronous.
On Entry
a
the sparse matrix.
A variable of type psb_Tspmat_type.
Scope: local.
diag
Include diagonals up to this one; diag=1 means the first superdiagonal,
diag=-1 means the first subdiagonal. Default 0.
imin,imax,jmin,jmax
Minimum and maximum row and column indices.
Type: optional.
rscale,cscale
Whether to rescale row/column indices. Type: optional.
On Return
l
A copy of the lower triangle of a.
A variable of type psb_Tspmat_type.
u
(optional) A copy of the upper triangle of a.
A variable of type psb_Tspmat_type.
info
Return code.
call a%triu(u,info[,& & diag,imin,imax,jmin,jmax,rscale,cscale,l])
Returns the upper triangular part of submatrix A(imin:imax,jmin:jmax),
optionally rescaling row/col indices to the range 1:imax-imin+1,1:jmax-jmin+1,
and returing the complementary lower triangle.
Type:
Asynchronous.
On Entry
a
the sparse matrix.
A variable of type psb_Tspmat_type.
Scope: local.
diag
Include diagonals up to this one; diag=1 means the first superdiagonal,
diag=-1 means the first subdiagonal. Default 0.
imin,imax,jmin,jmax
Minimum and maximum row and column indices.
Type: optional.
rscale,cscale
Whether to rescale row/column indices. Type: optional.
On Return
u
A copy of the upper triangle of a.
A variable of type psb_Tspmat_type.
l
(optional) A copy of the lower triangle of a.
A variable of type psb_Tspmat_type.
info
Return code.
call psb_set_mat_default(a)
Type:
Asynchronous.
On Entry
a
a variable of class(psb_T_base_sparse_mat) requesting a new default
storage format.
Type: required.
call a%clone(b,info)
Type:
Asynchronous.
On Entry
a
the sparse matrix.
Scope: local.
On Return
b
A copy of the input object.
info
Return code.
psb_dupl_ovwrt_
Duplicate coefficients should be overwritten (i.e. ignore duplications)
psb_dupl_add_
Duplicate coefficients should be added;
psb_dupl_err_
Duplicate coefficients should trigger an error conditino
psb_upd_dflt_
Default update strategy for matrix coefficients;
psb_upd_srch_
Update strategy based on search into the data structure;
psb_upd_perm_
Update strategy based on additional permutation data (see tools routine description).
The psb_T_vect_type data structure encapsulates the dense vectors in a way similar to sparse matrices, i.e. including a base type psb_T_base_vect_type. The user will not, in general, access the vector components directly, but rather via the routines of sec. 6. Among other simple things, we define here an extraction method that can be used to get a full copy of the part of the vector stored on the local process.
The type declaration is shown in figure 3 where T is a placeholder for the data
type and precision variants
I
Integer;
S
Single precision real;
D
Double precision real;
C
Single precision complex;
Z
Double precision complex.
The actual data is contained in the polymorphic component v%v; the separation between
the application and the actual data is essential for cases where it is necessary to link
to data storage made available elsewhere outside the direct control of the
compiler/application, e.g. data stored in a graphics accelerator’s private
memory.
type psb_T_base_vect_type TYPE(KIND_), allocatable :: v(:) end type psb_T_base_vect_type type psb_T_vect_type class(psb_T_base_vect_type), allocatable :: v end type psb_T_vect_type
nr = v%get_nrows()
Type:
Asynchronous.
On Entry
v
the dense vector
Scope: local
On Return
Function value
The number of rows of dense vector v.
memory_size = v%sizeof()
Type:
Asynchronous.
On Entry
v
the dense vector
Scope: local
On Return
Function value
The memory occupation in bytes.
call v%set(alpha[,first,last]) call v%set(vect[,first,last]) call v%zero()
Type:
Asynchronous.
On Entry
v
the dense vector
Scope: local
alpha
A scalar value.
Scope: local
Type: required
Intent: in.
Specified as: a number of the data type indicated in Table 1.
first,last
Boundaries for setting in the vector.
Scope: local
Type: optional
Intent: in.
Specified as: integers.
vect
An array
Scope: local
Type: required
Intent: in.
Specified as: a number of the data type indicated in Table 1.
Note that a call to v%zero() is provided as a shorthand, but is equivalent to a call
to v%set(zero) with the zero constant having the appropriate type and
kind.
On Return
v
the dense vector, with updated entries
Scope: local
extv = v%get_vect([n])
Type:
Asynchronous.
On Entry
v
the dense vector
Scope: local
n
Size to be returned
Scope: local.
Type: optional; default: entire vector.
On Return
Function value
An allocatable array holding a copy of the dense vector contents. If the argument n is specified, the size of the returned array equals the minimum between n and the internal size of the vector, or 0 if n is negative; otherwise, the size of the array is the same as the internal size of the vector.
call x%clone(y,info)
Type:
Asynchronous.
On Entry
x
the dense vector.
Scope: local.
On Return
y
A copy of the input object.
info
Return code.
Our base library offers support for simple well known preconditioners like Diagonal Scaling or Block Jacobi with incomplete factorization ILU(0).
A preconditioner is held in the psb_prec_type data structure reported in
figure 4. The psb_prec_type data type may contain a simple preconditioning matrix
with the associated communication descriptor.The internal preconditioner is
allocated appropriately with the dynamic type corresponding to the desired
preconditioner.
type psb_Tprec_type class(psb_T_base_prec_type), allocatable :: prec end type psb_Tprec_type
Among the tools routines of sec. 6, we have a number of sorting utilities; the heap sort is implemented in terms of heaps having the following signatures:
psb_T_heap
: a heap containing elements of type T, where T can be i,s,c,d,z for
integer, real and complex data;
psb_T_idx_heap
: a heap containing elements of type T, as above, together with an integer index.
Given a heap object, the following methods are defined on it:
init
Initialize memory; also choose ascending or descending order;
howmany
Current heap occupancy;
insert
Add an item (or an item and its index);
get_first
Remove and return the first element;
dump
Print on file;
free
Release memory.
These objects are used in AMG4PSBLAS to implement the factorization algorithms.